김유정(Yoojung Kim)

1. 분위수의 정의

분위수는 모집단이나 표본의 전체 돗수를 크기 순으로 p등분시키는 (p-1)개의 등분값을 말한다. 만약에 우리가 어떤 확률 분포의 CDF(Cumulative Distribution Function)를 알면 분위수를 쉽게 구할 수 있다. CDF의 역함수가 분위수이기 때문이다. 아래의 그림을 보면 직관적으로 이해할 수 있다. 확률 분포를 전구간 적분하면 1이므로 CDF의 범위는 0부터 1을 가지고, CDF의 역함수를 취하면 해당 y값에 해당하는 x값이 분위수이기 때문이다.

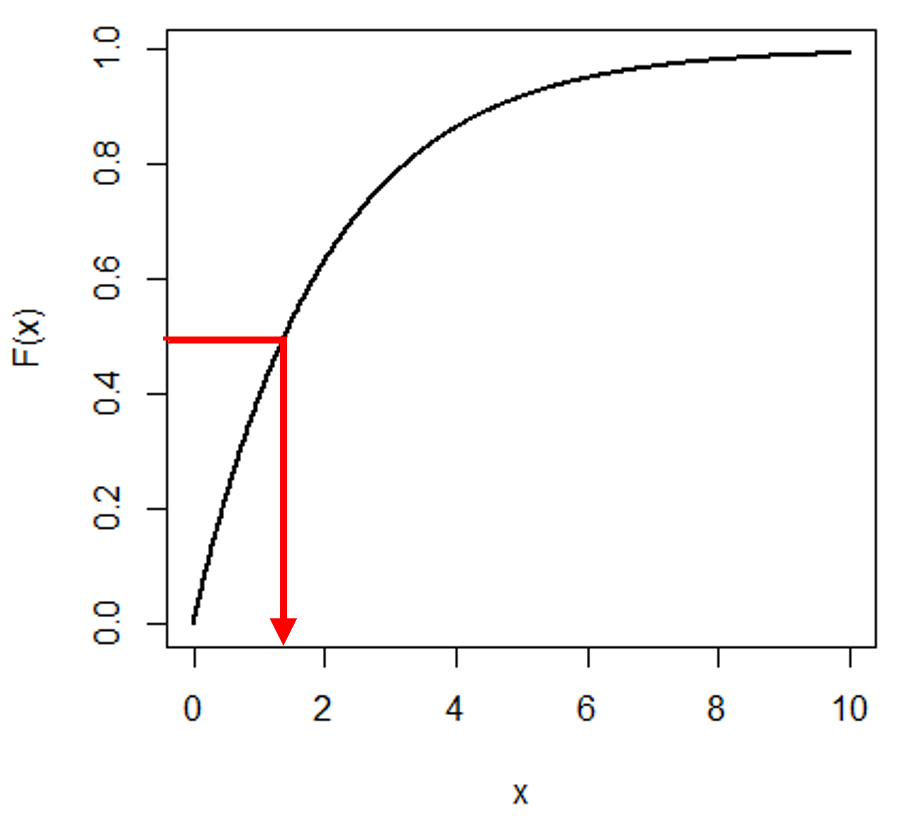
하지만 어떤 확률분포의 CDF를 모르면 어떻게 할까? 이럴 때 우리는 순서통계량을 이용할 수 있다. 어떤 확률분포 ${X_1, X_2, …, X_n}$ 의 순서통계량을 ${X_{(1)}, X_{(2)}, …, X_{(n)}}$라고 하면, 우리는 분위수를 아래와 같이 표현할 수 있다. 여기서 n=표본수, p=구하고자 하는 분위수, m=임의의 상수이다. 향후 우리는 설명의 편의성을 위해 아래 $\gamma$에서 정수 부분을 $j$, 소수 부분을 $g$라고 한다. (하지만 $\gamma$의 정의가 $np+m$에서 $np+m$의 정수 부분을 뺀 것이므로 $\gamma=g$라고 생각해도 무방함)

\[\gamma = (np+m) - \left \lfloor np+m \right \rfloor (0 \leq \gamma \leq 1)\]

위에서 정의한 $\gamma$를 이용해 분위수 함수를 아래와 같이 나타낸다.

\[Q(p) = (1-\gamma) X_{(j)} + \gamma X_{(j+1)} \qquad (\frac{j-m}{n} \leq p \leq \frac{j-m+1}{n})\]

즉 정리하자면, $p$분위수는 $\gamma$값으로 조정된 순서통계량 $X_{(j)}$와 $X_{(j+1)}$ 사이의 값을 의미하는 것이다. 이제 다음 장에서는 위에서 정의한 $\gamma$와 분위수 함수를 이용하여 분위수를 구하는 9가지 방법에 대해 알아보자.

2. 분위수를 구하는 9가지 방법

위의 순서통계량과 분위수 함수를 활용해 분위수를 구하는 9가지 방법에 대해 알아보자.

1) Type1

가장 오래되고 학술적인 정의인 type1 방법은 $\gamma$에서 $m=0$으로 하고 $np$가 정수인 경우($g=0$)와 정수가 아닌 경우($g=0$)로 구분한다. 이 때 $\gamma$는 아래와 같이 정의된다.

\[\gamma= \begin{cases} 1\quad(g>0)\\ 0\quad(g=0) \end{cases}\]

위 식을 분위수 함수에 적용하면, 분위수 함수는 아래와 같이 표현할 수 있다.

\[Q(p)= \begin{cases} X_{(j+1)}\quad(g>0)\\ X_{(j)}\quad(g=0) \end{cases} \quad \frac{j}{n}\leq p < \frac{j+1}{n}\]

만일 $p=0$인 경우에는 $Q=X_{(1)}$을, $p=1$인 경우에는 $Q=X_{(n)}$을 반환한다. 이를 R코드 구현하면 아래와 같다.

# data = 분포
# p = 구하고자 하는 분위수
type1 <- function(data, p) {
  data <- sort(data)
  n = length(data)
  if (p==0) {
    Qs<-data[1]
  } else if (p==1) {
    Qs<-data[n]
  } else {
    m = 0
    j = floor(n*p+m) # 정수부분
    g = (n*p+m) - j # 소수부분
    Qs = ifelse(g>0, data[j+1], data[j])
  }
  return(Qs)
}

2) Type2

Type2 방법은 type1 방법과 유사하다. 다만, type2에서는 $np$가 정수인 경우(즉 $g=0$인 경우), $\gamma$가 $0$이 아닌 $\frac{1}{2}$이 된다

\[\gamma= \begin{cases} 1\quad(g>0)\\ \frac{1}{2}\quad(g=0) \end{cases}\]

위 식을 분위수 함수에 적용하면, 분위수 함수는 아래와 같이 표현할 수 있다.

\[Q(p)= \begin{cases} X_{(j+1)}\quad(g>0)\\ \frac{X_{(j)}+X_{(j+1)}}{2}\quad(g=0) \end{cases} \quad \frac{j}{n}\leq p < \frac{j+1}{n}\]

즉 type2 방법에서 분위수는 $np$가 정수일 때, 순서통계량 $X_{(j)}$과 $X_{(j+1)}$의 평균값임을 알 수 있다. 만일 $p=0$인 경우에는 $Q=X_{(1)}$을, $p=1$인 경우에는 $Q=X_{(n)}$을 반환한다. 이를 R코드 구현하면 아래와 같다.

# data = 분포
# p = 구하고자 하는 분위수
type2 <- function(data, p) {
  data <- sort(data)
  n = length(data)
  if (p==0) {
    Qs<-data[1]
  } else if (p==1) {
    Qs<-data[n]
  } else {
    m = 0 
    j = floor(n*p+m) #정수부분
    g = (n*p+m) - j #소수부분
    Qs = ifelse(g>0, data[j+1],(data[j] + data[j+1])/2)
  }
  return(Qs)
}

3) Type3

Type3 방법에서는 $m=-\frac{1}{2}$로 두고 $np-\frac{1}{2}$이 짝수인 경우와 그 이외의 경우로 구분하여 가중치 $\gamma$를 아래와 같이 정의한다.

\[\gamma= \begin{cases} 0\quad(g>0 \, and \, j=even)\\ 1\quad(else) \end{cases}\]

위 식을 분위수 함수에 적용하면, 분위수 함수는 아래와 같이 표현할 수 있다.

\[Q(p)= \begin{cases} X_{(j)}\quad(g>0 \, and \, j=even)\\ X_{(j+1)}\quad(else) \end{cases} \quad \frac{j+\frac{1}{2}}{n}\leq p < \frac{j+\frac{3}{2}}{n}\]

만일 $p\leq\frac{\frac{1}{2}}{n}$인 경우에는 $Q=X_{(1)}$이 된다. 이를 R코드 구현하면 아래와 같다.

# data = 분포
# p = 구하고자 하는 분위수
type3 <- function(data, p) {
  data <- sort(data)
  n = length(data)
  if (p<=(1/2)/n) {
    Qs<-data[1]
  } else {
    m = -0.5 
    j = floor(n*p+m) # 정수부분
    g = (n*p+m) - j # 소수부분
    Qs = ifelse((g==0 & j%%2==0), data[j], data[j+1] )
  }
  return(Qs)
}

4) Type4

Type4 방법은 Type1 방법에 선형보간법을 결합한 방법이다. Type1과 같이 $m=0$을 대입하면 아래와 같은 $\gamma$값을 얻을 수 있다.

\[\gamma=np-\left \lfloor np \right \rfloor = np-j = g\]

위 $\gamma$를 분위수 함수에 적용하면, 분위수 함수는 아래와 같이 표현할 수 있다.

\[Q(p)= (1-\gamma)X_{(j)}+\gamma X_{(j+1)} \quad \frac{j}{n}\leq p < \frac{j+1}{n}\]

즉, $np$가 정수가 아닐 때는 $\gamma$값에 따라 순서통계량 $X_{(j)}$와 $X_{(j+1)}$ 사이의 값을 반환하게 되는 것이다. 만일 $p<\frac{1}{n}$인 경우에는 $Q=X_{(1)}$이 되고, $p=1$인 경우, $Q=X_{(n)}$이 된다. 이를 R코드 구현하면 아래와 같다.

# data = 분포
# p = 구하고자 하는 분위수
type4 <- function(data, p) {
  data <- sort(data)
  n = length(data)
  if (p<1/n) {
    Qs<-data[1]
  } else if (p==1) { 
    Qs<-data[n]
  } else {
    m = 0 
    j = floor(n*p+m) # 정수부분
    g = (n*p+m) - j # 소수부분
    Qs = (1-g)*data[j] + g*data[j+1]
  }
  return(Qs)
}

5) Type5

Type5 방법에서는 $m=\frac{1}{2}$을 대입해 아래와 같은 $\gamma$를 이용한다.

\[\gamma=(np+\frac{1}{2})-\left \lfloor np+\frac{1}{2} \right \rfloor = (np+\frac{1}{2})-j = g\]

위 $\gamma$를 분위수 함수에 적용하면, 분위수 함수는 아래와 같이 표현할 수 있다.

\[Q(p)= (1-\gamma)X_{(j)}+\gamma X_{(j+1)} \quad \frac{j-\frac{1}{2}}{n}\leq p < \frac{j+\frac{1}{2}}{n}\]

만일 $p<\frac{\frac{1}{2}}{n}$인 경우에는 $Q=X_{(1)}$이 되고, $p\geq\frac{n-\frac{1}{2}}{n}$인 경우, $Q=X_{(n)}$이 된다. 이를 R코드 구현하면 아래와 같다.

# data = 분포
# p = 구하고자 하는 분위수
type5 <- function(data, p) {
  data <- sort(data)
  n = length(data)
  if (p<(1/2)/n) {
    Qs<-data[1]
  } else if (p>=(n-1/2)/n){ 
    Qs<-data[n]
  } else {
    m = 0.5 
    j = floor(n*p+m) # 정수부분
    g = (n*p+m) - j # 소수부분
    Qs = (1-g)*data[j] + g*data[j+1]
  }
  return(Qs)
}

6) Type6

Type5 방법에서는 $m=p$을 대입해 아래와 같은 $\gamma$를 이용한다.

\[\gamma=(np+p)-\left \lfloor np+p \right \rfloor = (np+p)-j = g\]

위 $\gamma$를 분위수 함수에 적용하면, 분위수 함수는 아래와 같이 표현할 수 있다.

\[Q(p)= (1-\gamma)X_{(j)}+\gamma X_{(j+1)} \quad \frac{j}{n+1}\leq p < \frac{j+1}{n+1}\]

만일 $p<\frac{1}{n+1}$인 경우에는 $Q=X_{(1)}$이 되고, $p\geq\frac{n}{n+1}$인 경우, $Q=X_{(n)}$이 된다. 이를 R코드 구현하면 아래와 같다.

# data = 분포
# p = 구하고자 하는 분위수
type6 <- function(data, p) {
  data <- sort(data)
  n = length(data)
  if (p<1/(n+1)) {
    Qs <- data[1]
  } else if (p>=n/(n+1)){ 
    Qs <- data[n]
  } else {
    m = p 
    j = floor(n*p+m) # 정수부분
    g = (n*p+m) - j # 소수부분
    Qs <- (1-g)*data[j] + g*data[j+1]
  }
  return(Qs)
}

7) Type7

Type7 방법에서는 $m=1-p$을 대입해 아래와 같은 $\gamma$를 이용한다.

\[\gamma=(np+1-p)-\left \lfloor np+1-p \right \rfloor = (np+1-p)-j = g\]

위 $\gamma$를 분위수 함수에 적용하면, 분위수 함수는 아래와 같이 표현할 수 있다.

\[Q(p)= (1-\gamma)X_{(j)}+\gamma X_{(j+1)} \quad \frac{j-1}{n-1}\leq p < \frac{j}{n-1}\]

만일 $p=1$인 경우, $Q=X_{(n)}$이 된다. 이를 R코드 구현하면 아래와 같다.

# data = 분포
# p = 구하고자 하는 분위수
type7 <- function(data, p) {
  data <- sort(data)
  n = length(data)
  if (p==1) {
    Qs <- data[n]
  } else {
    m = 1-p 
    j = floor(n*p+m) # 정수부분
    g = (n*p+m) - j # 소수부분
    Qs <- (1-g)*data[j] + g*data[j+1]
  }
  return(Qs)
}

8) Type8

Type8 방법에서는 $m=\frac{1}{3}(p+1)$을 대입해 아래와 같은 $\gamma$를 이용한다.

\[\gamma=(np+\frac{1}{3}(p+1))-\left \lfloor np+\frac{1}{3}(p+1) \right \rfloor = (np+\frac{1}{3}(p+1))-j = g\]

위 $\gamma$를 분위수 함수에 적용하면, 분위수 함수는 아래와 같이 표현할 수 있다.

\[Q(p)= (1-\gamma)X_{(j)}+\gamma X_{(j+1)} \quad \frac{j-\frac{1}{3}}{n+\frac{1}{3}}\leq p < \frac{j+\frac{2}{3}}{n+\frac{1}{3}}\]

만일 $p<\frac{\frac{2}{3}}{n+\frac{1}{3}}$인 경우 $Q=X_{(1)}$이 되고, $p>\frac{n-\frac{1}{3}}{n+\frac{1}{3}}$인 경우 $Q=X_{(n)}$이 된다. 이를 R코드 구현하면 아래와 같다.

# data = 분포
# p = 구하고자 하는 분위수
type8 <- function(data, p) {
  data <- sort(data)
  n = length(data)
  if (p<(2/3)/(n+1/3)) {
    Qs <- data[1]
  } else if (p>=(n-1/3)/(n+1/3)){
    Qs <- data[n]
  } else {
    m = (p+1)/3
    j = floor(n*p+m) # 정수부분
    g = (n*p+m) - j # 소수부분
    Qs <- (1-g)*data[j] + g*data[j+1]
  }
  return(Qs)
}

9) Type9

마지막으로 Type9 방법에서는 $m=\frac{1}{4}(p+\frac{3}{2})$을 대입해 아래와 같은 $\gamma$를 이용한다.

\[\gamma=(np+\frac{1}{4}(p+\frac{3}{2}))-\left \lfloor np+\frac{1}{4}(p+\frac{3}{2}) \right \rfloor = (np+\frac{1}{4}(p+\frac{3}{2}))-j = g\]

위 $\gamma$를 분위수 함수에 적용하면, 분위수 함수는 아래와 같이 표현할 수 있다.

\[Q(p)= (1-\gamma)X_{(j)}+\gamma X_{(j+1)} \quad \frac{j-\frac{3}{8}}{n+\frac{1}{4}}\leq p < \frac{j+\frac{5}{8}}{n+\frac{1}{4}}\]

만일 $p<\frac{\frac{5}{8}}{n+\frac{1}{4}}$인 경우 $Q=X_{(1)}$이 되고, $p\geq\frac{n-\frac{3}{8}}{n+\frac{1}{4}}$인 경우 $Q=X_{(n)}$이 된다. 이를 R코드 구현하면 아래와 같다.

# data = 분포
# p = 구하고자 하는 분위수
type9 <- function(data, p) {
  data <- sort(data)
  n = length(data)
  if (p<(5/8)/(n+1/4)) {
    Qs <- data[1]
  } else if (p>=(n-3/8)/(n+1/4)){
    Qs <- data[n]
  } else {
    m = (p+(3/2))/4
    j = floor(n*p+m) # 정수부분
    g = (n*p+m) - j # 소수부분
    Qs <- (1-g)*data[j] + g*data[j+1]
  }
  return(Qs)
}

3. 간단한 simulation

1) 타입별 비교

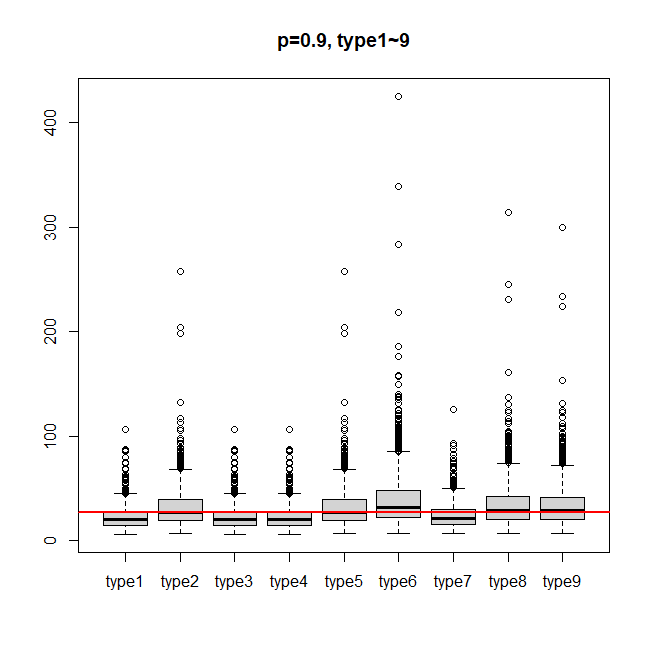
위에서 정리한 9개 type의 분위수 함수를 기준으로 간단한 실험을 해보았다. 사용할 분포는 lognormal distribution으로, $Y=logX\sim N(2, 1^2)$로 세팅 후, 각 타입별로 분위수를 1000개씩 생성해 boxplot을 그려본 결과는 아래와 같다. boxplot을 보면, type6가 다른 타입들에 비해 편차가 크다는 것을 알 수 있었다.

p = 0.9 # 구하고자 하는 분위수
iter = 1000 # 반복 횟수

out10_1=c(); out10_2=c(); out10_3=c()
out10_4=c(); out10_5=c(); out10_6=c()
out10_7=c(); out10_8=c(); out10_9=c()

for (i in 1:iter) {
  dist = exp(rnorm(n=10, mean=2, sd=1)) # lognormal 분포 (n=10)
  out10_1 = c(out10_1, type1(dist, p))
  out10_2 = c(out10_2, type2(dist, p))
  out10_3 = c(out10_3, type3(dist, p))
  out10_4 = c(out10_4, type4(dist, p))
  out10_5 = c(out10_5, type5(dist, p))
  out10_6 = c(out10_6, type6(dist, p))
  out10_7 = c(out10_7, type7(dist, p))
  out10_8 = c(out10_8, type8(dist, p))
  out10_9 = c(out10_9, type9(dist, p))
}

# boxplot 그리기
boxplot(out10_1, out10_2, out10_3,
        out10_4, out10_5, out10_6,
        out10_7, out10_8, out10_9,
        main="p=0.9, type1~9",
        names=c("type1", "type2", "type3", "type4", "type5", "type6", "type7", "type8", "type9"))
abline(h=exp(qnorm(0.9, 2, 1)), col="red", lwd=2) # 실제 90분위수 추가

2) 표본수 별 비교

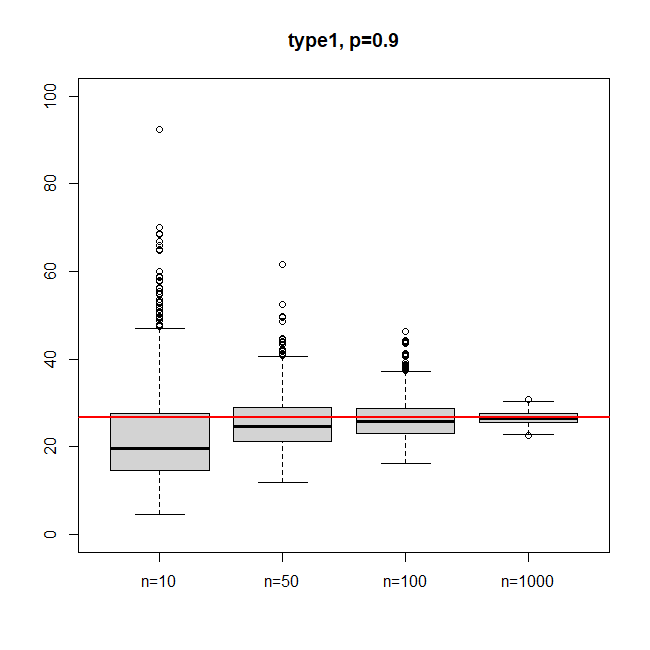
이번에는 위와 동일한 분포를 이용하되, 분위수 함수는 type1으로 고정하고 표본수를 $n=10, 50, 100, 1000$으로 변화를 주면서 실험해 보았다. 아래의 boxplot을 보면, $n$이 커질수록 편차가 작아져 실제 90분위수를 더 잘 추정한다는 것을 알 수 있다.

n = c(10, 50, 100, 1000) # 표본수 변화 주기
p = 0.9 # 90분위수 구하기
iter = 1000 # 반복 횟수

out10 = c(); out50 = c()
out100 = c(); out1000 = c()
for (i in 1:iter) {
  norm10 = exp(rnorm(n=n[1], mean=2, sd=1))
  norm50 = exp(rnorm(n=n[2], mean=2, sd=1))
  norm100 = exp(rnorm(n=n[3], mean=2, sd=1))
  norm1000 = exp(rnorm(n=n[4], mean=2, sd=1))
  out10 = c(out10, type1(norm10, p))
  out50 = c(out50, type1(norm50, p))
  out100 = c(out100, type1(norm100, p))
  out1000 = c(out1000, type1(norm1000, p))
}

boxplot(out10, out50, out100, out1000, ylim=c(0, 100),
        main="type1, p=0.9",
        names=c("n=10", "n=50", "n=100", "n=1000"))
abline(h=exp(qnorm(0.9, mean=2, sd=1)), col="red", lwd=2) # 실제 90분위수 추가

4. 정리

1학기 시뮬레이션 수업 때 발표했던 논문 리뷰를 다시 정리해서 올린다. 이전까지는 ‘분위수가 그냥 분위수지…‘라는 단순한 생각을 가지고 있었는데 이 논문을 리뷰하면서 분위수를 구하는 방법이 무려 9가지 존재했다는 걸 알게 되었다. 사실 9가지 방법은 서로 크게 다르지는 않다. $m$에 어떤 값을 대입하는지에 따라 분위수 함수가 조금씩 달라지는 정도이다. 그러나 각 통계 프로그램마다 default로 되어 있는 분위수 정의가 다르기도 하고(R은 type7, Minitab과 SPSS는 type6, SAS는 type3), 여러 논문에 이용되는 방법도 각기 다양하기 때문에 총정리를 하는 데 의의를 둔 것 같다.
내가 리뷰했던 논문에서는 지수분포(극단값 존재, 연속형, 비대칭)로 9가지 방법에 대해 표본수($n$)과 모수($\lambda$)를 다양하게 바꿔가면서 실제 R프로그램 내장함수와 MSE를 구하는 모의실험까지 진행했었으나 여기에서는 생략했다.

[Reference]

  • 허윤숙, (2017), 지수 분포를 따르는 자료의 분위수 계산 방법 비교, 동국대학교 석사학위논문
  • Langford, E. (2006). Quartiles in Elementary Statistics, URL: http://www.amstat.org/publications/jse/v14n3/ langford.html.
  • Hyndman. R. J., and Fan. Y, (1996), Sample quantiles in statistical packages, American Statistician, Vol.50 No.4 pp.361-365

You may also enjoy

첫 포스팅 테스트용

처음 깃허브 페이지 만들었다.아직 허전하지만 꾸준히 관리해서 풍부하게 만들어야지. 깃허브에 커밋하는 걸 개발자들은 ‘잔디심기’라고 하던데, 아직 초반이라 이런 저런 설정을 많이 바꿔서 그런지 잔디의 색상이 굉장히 진하다. 진한 잔디 색상만큼 열심히 커밋했다는 게 아니고 그냥 시행착...